In the financial world, the effective assessment of the financial performance of investments is of great importance. There are several methods available to investors for this purpose, including Simple Return and Time-Weighted Return. Below we take a look at both methods, their advantages, disadvantages and areas of application.
Simple Return
The Simple Return is useful when investors need a quick and easy-to-understand calculation of returns. It is particularly suitable for one-off investments over a fixed period of time, without further deposits or withdrawals. The following types of investments can be evaluated well with the Simple Return:
- Fixed-income investments: Investments such as time deposits or bonds that offer a fixed interest rate over a fixed period of time can be well assessed for profitability using the simple rate of return.
- Real estate purchases: When investing in real estate, the simple rate of return can help to calculate the increase in value of a property over a certain period of time in relation to the original purchase price.
To calculate the Simple Return, we use the following formula:
(Current value of investment – Net investment) / Net investment
The net investment is calculated from your first deposit, plus all deposits, minus any withdrawals.
The simple return method reaches its limits when it comes to evaluating performance over several periods and for deposits and withdrawals. Moreover, it cannot accurately represent the effect of compound interest. For an investment in a portfolio with intervening deposits or withdrawals, it can therefore be difficult to determine how your portfolio has performed. We have therefore decided to focus on a different method: Time-Weighted Return (or TWR).
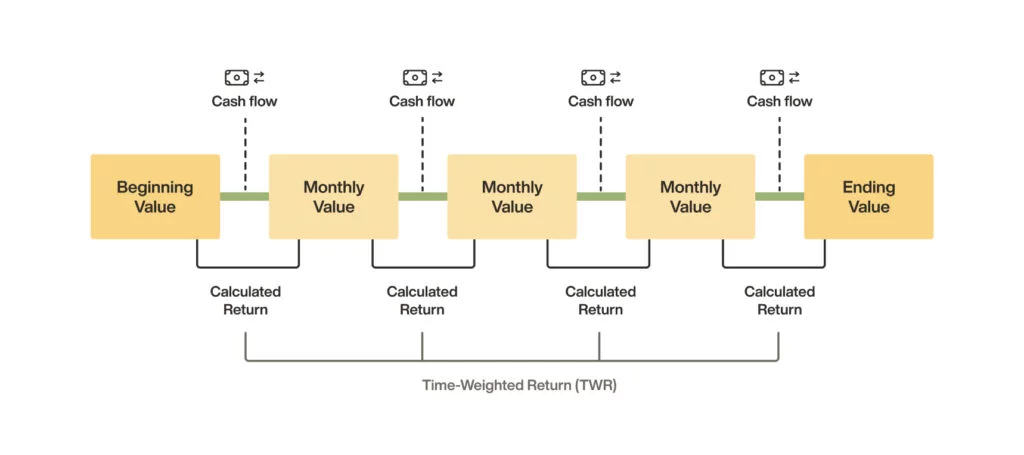
Time-Weighted Return (TWR)
The Time-Weighted Return is very useful as a basis for evaluating investments, as it compensates for the disadvantages of the Simple Return method. Unlike the Simple Return, the TWR takes into account the changes in invested capital over time. The time-weighted return therefore gives you a holistic view of your portfolio’s gains and losses. This is because the TWR neutralises the impact of inflows and outflows on the actual growth of the investment.
The TWR is therefore particularly useful when evaluating the performance of investment portfolios in which cash inflows and outflows occur. By eliminating the impact of cash inflows and outflows, the TWR provides a more meaningful assessment of investment performance as it represents only the actual percentage growth and performance of your portfolio on a daily basis.
To calculate the TWR, we use the following (simplified) formula:
(1 + Percentage Return Sub-Period 1) x
(1 + Percentage Return Sub-Period 2) x
(1 + Percentage Return Sub-Period 3) x
(…) – 1.
The TWR divides the investment period into sub-periods depending on when deposits or withdrawals were made and then calculates the return for each sub-period. The returns for each sub-period are combined using a special mathematical method (compounding) to calculate the total return for the entire investment period.
Can there be a difference between the simple and time-weighted return?
Yes, there may be a difference between the simple and time-weighted returns if there have been large inflows or outflows in the meantime.
- Imagine you invest CHF 1,000 on 1 January.
- In the first six months (period 1) your portfolio gains 10% in value based on the initial investment. The value after period 1 is therefore CHF 1,100.
- After six months you pay in CHF 1,000.
- In the second half of the year, your portfolio gains an additional CHF 210. This corresponds to a growth of 10 % in period 2.
- The value at the end of the year is therefore CHF 2,310.
Calculation of the simple return
(Current value of investment – Net investment) / Net investment =
(2,310 – 2,000) / 2,000 = 0.155 = 15.5%
The simple return after 12 months would be 15.5% in this example.
Calculation of the time-weighted return
(1 + Percentage Return Sub-Period 1) x (1 + Percentage Return Sub-Period 2) – 1 =
(1 + 0.1) x (1 + 0.1) – 1 = 0.21 = 21%
The TWR after 12 months would be 21% in this example.
How is it possible to have a negative simple return while the TWR is positive?
The simple return can be negative while the TWR is positive. Example: If you have a positive percentage return on a small investment in the first six months, both the simple return and the TWR will be positive. However, if you make a large deposit the next month (while the market is moving negatively), this will have a much greater impact on the simple return than on the TWR.
- Imagine you invest CHF 1,000 on 1 January.
- In the first six months (period 1) your portfolio makes a profit of 10% based on the initial investment.
- After six months you pay in CHF 1,000.
- Due to the market development, the value of your portfolio has slightly decreased and amounts to CHF 1,995 at the end of the year.
- In the second half of the year, your portfolio loses CHF 105, which corresponds to a decline of 5 % in period 2.
Calculation of the simple return
(Current value of investment – Net investment) / Net investment =
(1,995 – 2,000) / 2,000 = -0.0025 = -0.25%
The simple return after 12 months would be -0.25% in this example.
Calculation of the time-weighted return
(1 + Percentage Return Sub-Period 1) x (1 + Percentage Return Sub-Period 2) – 1 =
(1 + 0.1) x (1 – 0.05) – 1 = 0.045 = 4.5%
The TWR after 12 months would be 4.5% in this example.
Why does Inyova use TWR?
An Inyova investment is designed for the long term. In order to minimise the effect of price fluctuations and to diversify the portfolio over time, many impact investors regularly deposit money into their Inyova account. Therefore, we primarily use the TWR method for the presentation of performance, because it allows us to take into account the effects of deposits and withdrawals.
The time-weighted return makes it possible to see the actual performance of the portfolio, regardless of the individual investment and withdrawal decisions of the impact investors. This makes it easier to compare the performance of different portfolios over time.
Conclusion
The choice between Simple and Time-Weighted Returns depends on several factors, including the type of investment, the time period and the specific needs of the investor. While the Simple Return offers a quick assessment, the TWR offers a more detailed and precise analysis of investment portfolios.



